préambule-Attention, Ce post est long car il suit une démarche scientifique
-Si vous avez le courage de tout lire, vous serez convaincu et vous appliquerez ce principe (j’espère en tout cas)
-sinon, il faudra me croire sur parole
-
sommaire :- introduction
- mise en situation
- pourquoi ?
- comment faire ?
-solution 1
-solution 2
-réglage
- mise en pratique rapide
-conclusion
introduction :Quand mon prof de méca m'a dit :
mon prof de méca a écrit:les roues d'une voiture ne braque pas du même angle
Il m'a lancé une sorte de défis.
En fouillant un peu sur le site, je n'ai vu quasiment aucune direction similaire ( ackermann ) sur les MOCs et sur les set officiels Lego.
Bref, il est temps de mettre ça au clair.
Qu'est ce qu'une directions ?
Wikipedia a écrit: La direction d'une automobile ou d'un véhicule routier en général, est l'ensemble des organes qui permet de modifier l'orientation de sa trajectoire et donc de prendre des virages.
Traduction en image. (j'en profite pour poser le vocabulaire)
 mise en pratique :
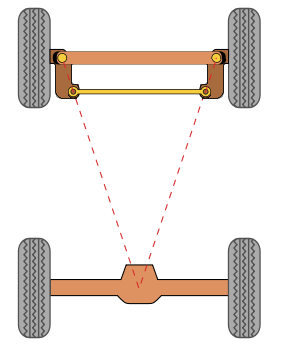
mise en pratique :Avant d'expliquer quoi que ce soit, nous allons comprendre quel est le problème des directions parallèles.
Réalisez rapidement un petit châssis comme sur la photos, il faut que les 4 roues soient directrices (4WS).

Faites le rouler avec les roues droites.
Ensuite, braquez les roues à fond en 4WS (pas en crabe).

Refaites rouler le châssis et observez.
Observation :Le châssis ne roule plus avec les roues braquées.
Conclusion :La direction parallèle présente beaucoup de frottements.
Pourquoi ?
Pourquoi ?Il faut savoir, chose peu connu, que les roues d'une voiture ne braque pas du même angle.
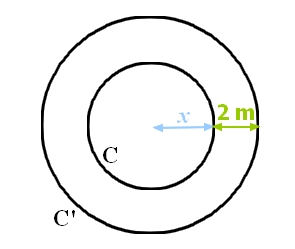
En effet, il faut que chaque roues du véhicule tourne selon des arcs de cercles concentriques (même centre) pour ne pas qu'elles s’écartent.
En vous épargnant de tracer le schéma, on obtient ça :
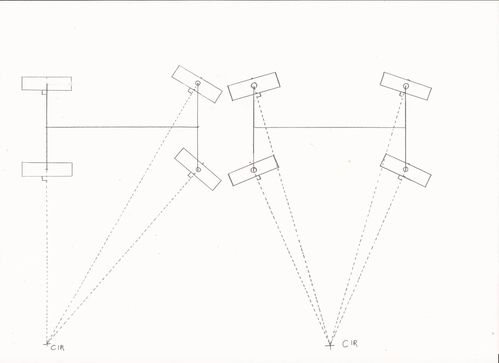
Ça alors ! Les roues ne doivent pas rester parallèles ! (eh oui, elle ne sont pas perpendiculaire à une même direction, si vous ne voyez pas très bien). De plus, c'est encore plus prononcé sur la direction 4WS si on tourne à fond.
Mais alors, comment faire ?
Comment faire ?J'ai un peu chercher sur internet mais je n'ai rien trouvé (j'aurais pu trouver la solution avec l'image de l'intro, mais ça m'a échapper).
Mais j'ai trouvé 2 solutions, dont l'une doit certainement être le vrai système.
Les deux n'ont pas la même intensité donc pas la même utilisation.
Solution 1 :Utilisation :
MOC large et assez court en longueur, 4WS
L'idée de base était de rompre avec la forme classique du parallélogramme. J'ai trouvé dans quel sens en faisant des tests.
Le principe est le suivant : réaliser un trapèze droit dont le petit coté parallèle est le plus proche du milieu du véhicule.
En image, ça donne ça : (note : la solution rouge est tout à fait valable, c'est juste pour monter qu'on peut mettre la crémaillère à l'extérieur)
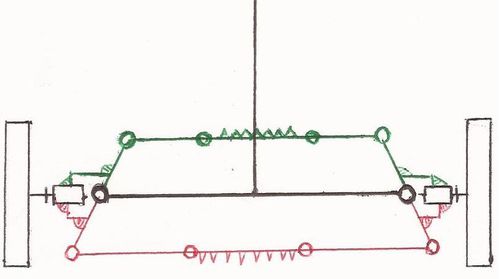


En lego, je vous conseil de réaliser vos porte fusée sur des liftarm en L

.
Personnellement, je préfère mettre la crémaillère à l'extérieur du véhicule pour me laisser la place de mettre les tringles .
Exemple de porte fusée assez costaux (pour MOC moyen):

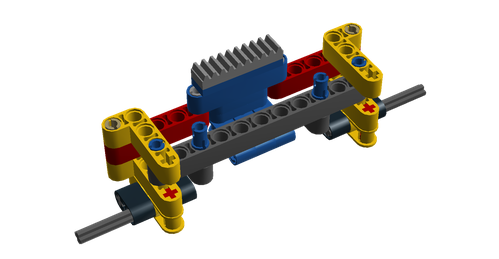
Preuve que ça marche sur mon
mon autocar :

Pour les ponts à portiques de l'Unimog

, il faudra utiliser des cross block plus long

pour une crémaillère interne, des connecteurs 1

pour une crémaillère externe, à la place d'un cross block simple
. Désolé, je n'ai pas les pièces pour vous l’illustrer mieux.
Solution 2 :Utilisation :
MOC assez effilé, beaucoup moins large que long.
C'est une solution dont j'ai du mal à l'expliquer. Je l'ai découverte par hasard en réalisant un mauvais jeu de tringle.
Le principe est le suivant : décaler la tringle vers l’intérieur du véhicule.
Traduction en image : (pareil, la solution rouge marche aussi bien que la verte)
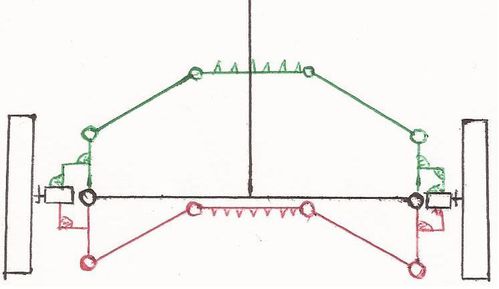


Pour les moyeux, vous pouvez ainsi utiliser les connecteurs classiques :

que je déconseil car il n'y a q'une liaison pivot (insuffisant).
Mais vous pouvez aussi utiliser les portes fusées préfabriqués comme cela :

Il vous faudra en revanche faire des tringles en combinant ces pièces :

Le problème de cette solution, c'est que si on élargis le châssis, il faudra décaler 2 fois la tringle vers l’intérieur pour compenser :
-la diminution de son effet
-et l'augmentation de la différence (voir réglage).
Dernier chose, il faut absolument que la crémaillère soit indépendante des tringle (pour les deux solutions), et qu'elle soit en liaison glissière avec le châssis.
Exemple de montage pratique :
 réglage :
réglage :Je n'ai pas de formule magique à vous proposer.
Mais il faut prendre en compte 2 variables :
La longueur et la largeur du rectangle formé par les points de pivot des roues directrices et la droite des roues fixes.
Plus le rapport largeur/longueur est grand, plus il faudra accentué la différence de braquages des roues, donc privilégier la solution 1.
Le meilleur moyen de faire ses réglage est de dessiner un schéma du MOC à l’échelle, et de tracer les droites comme sur mon schéma du début. Ensuite, vous chercher à tâtons les meilleurs meilleurs dimensions.
mise en pratique rapide :Vous n’êtes pas convaincu par mon blabla ?
Essayez le vous même !
Reprenez le châssis du début, et changez les moyeux par cela :


Refaites la même expérience et observez de nouveau.
 Observation :
Observation :Ça frotte beaucoup moins !
Comparez les deux directions en changeant alternativement la taille de la tringle. C'est saisissant !
Conclusion :C'est bon, vous êtes convaincu ?
Alors maintenant, faites moi plaisir et ne construisez que des directions ackermann.
Si vous avez des questions, n'hésitez pas car j'ai certainement oublié des choses, il y a tant à dire !
De même, si vous avez d'autre solutions, n'hésitez pas à les ajouter !









.gif)















 .
.


 , il faudra utiliser des cross block plus long
, il faudra utiliser des cross block plus long  pour une crémaillère interne, des connecteurs 1
pour une crémaillère interne, des connecteurs 1  pour une crémaillère externe, à la place d'un cross block simple
pour une crémaillère externe, à la place d'un cross block simple  . Désolé, je n'ai pas les pièces pour vous l’illustrer mieux.
. Désolé, je n'ai pas les pièces pour vous l’illustrer mieux.



 que je déconseil car il n'y a q'une liaison pivot (insuffisant).
que je déconseil car il n'y a q'une liaison pivot (insuffisant).




















 .
.


 ).
).
