Voilà bien longtemps que je n'ai pas publié un nouveau sujet sur le forum ! Ça me fait plaisir

Depuis que j'ai ralenti les Lego, je m'intéresse aux civilisations anciennes (Et oui, il y a un rapport, on va finir par revenir aux Lego...) Je me suis pris de passion pour les travaux de chercheurs comme Howard Crowhurst ou Quentin Leplat et je réalise aujourd'hui mes propres recherches. Quand on parle des ancien peuples, on pense tout de suite aux pyramides d'Égypte, aux alignements de Carnac, à Stonehenge, etc. Le mystère de ces constructions reste encore très grand, mais les travaux de chercheurs indépendants ont permis de montrer qu'une géométrie bien particulière sous tend la construction et le choix des emplacements de tous ces sites.
Cette géométrie peut être dite "modulaire" dans le sens où elle se fonde sur des modules carrés. Ainsi, au lieu de faire apparaître des angles de 10°, 15°, 30°, 60°, etc, elle va faire apparaître des angles définis par des rapports de nombres entiers. Par exemple, sur un quadrillage, si vous vous décalez de 2 vers la droite et que vous montez de 1, vous allez définir une pente de 26,565...° En mathématiques, on dira "arc-tangente de 1/2" et on notera cet angle arctan(1/2). Je ne vais pas rentrer dans les détails de où, comment et pourquoi on retrouve cette géométrie dans les constructions anciennes. Ce qui nous intéresse ici c'est que pour mes recherches j'ai étudié cette géométrie modulaire et il se trouve qu'elle s'applique aux Lego !
Et bien oui, comment sont définis les angles des wedges ? Avec des arc-tangentes de nombres entiers ! C'est une géométrie qu'on a du mal à utiliser avec nos systèmes de degrés et radians habituels. On ne nous apprend pas les formules qui régissent les arc-tangentes. Du coup, quand on a nos petites briques dans les mains, on tâtonne... Et bien c'est fini !
Je vais vous expliquer comment vous servir proprement des wedges ! (Rien que ça...)
Entre parenthèses, je ne suis même pas sûr que le designer TLG lambda ait conscience de ce que je vais vous montrer car à ma connaissance, aucun set ne propose les montages ci-dessous.
Anio, si tu corrobores ce que je pense, fais leur suivre les images, j'aurais plaisir à monter au Danemark les leur expliquer (Ça y est, le mec se sent plus...
 )
)En fait, il y a sans doute certains sets qui proposent ce genre de chose et que je ne connais pas, mais y a-t-il pour autant des AFOLs qui en ont pris conscience ?
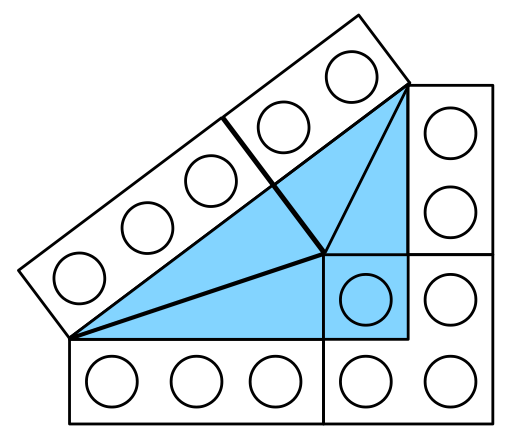
Allons-y : les angles définis par des arc-tangentes de rapports de nombres entiers sont tous en lien avec des triangles de Pythagore spécifiques. Pour rappel, un triangle de Pythagore est un triangle rectangle dont les longueurs des trois côtés sont exprimables en nombres entiers
Les angles arctan(1/2) et arctan(1/3) sont liés au triangle 3-4-5.
Les angles arctan(1/4) et arctan(3/5) sont liés au triangle 8-15-17.
Les angles arctan(1/6) et arctan(5/7) sont liés au triangle 12-35-37.
Je pourrais continuer la liste indéfiniment, mais ce sont ces trois là qui vont nous intéresser en Lego.
Voyez plutôt :
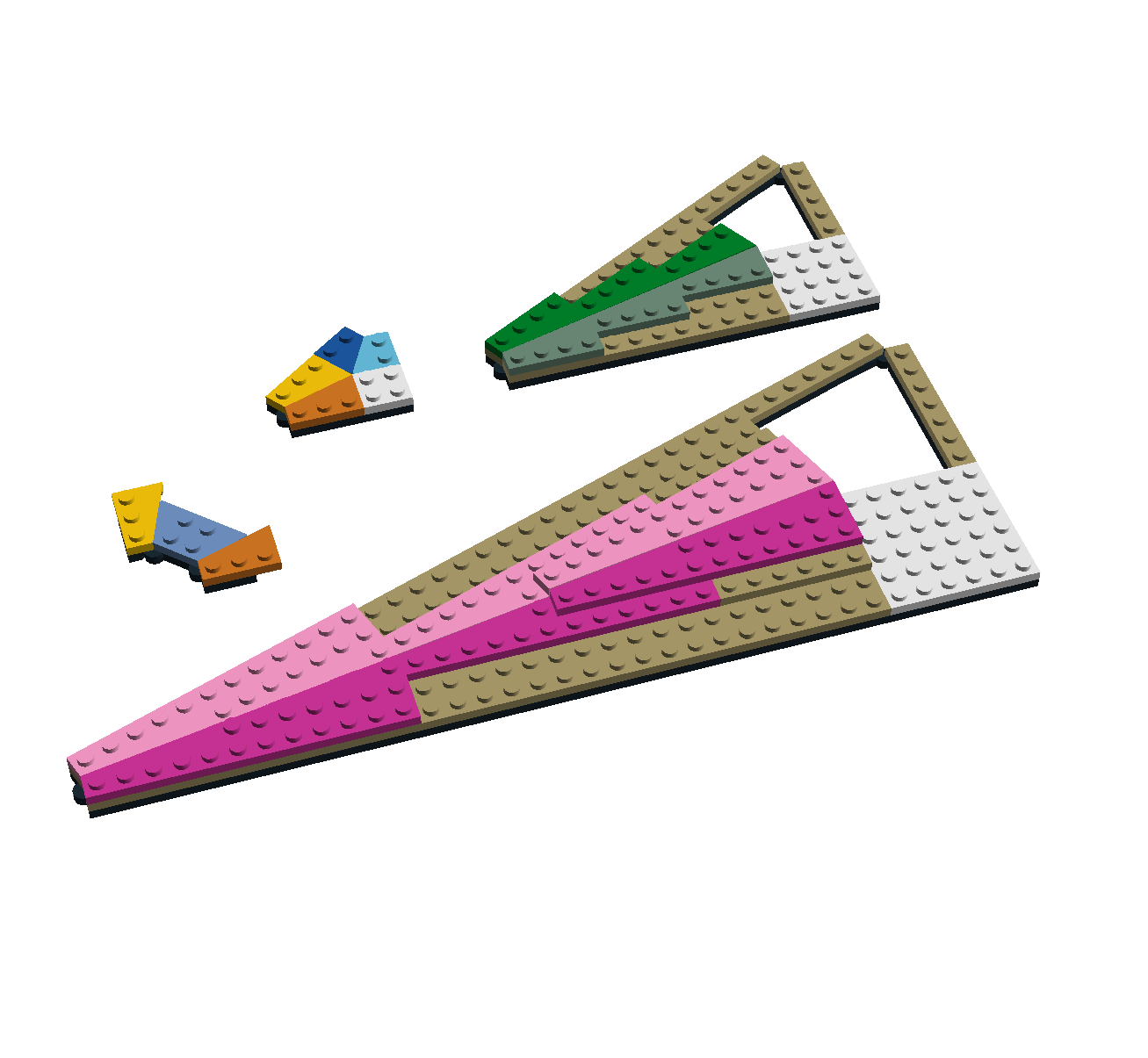
Observer simplement ces montages permet de comprendre des choses.
Pour moi, le montage mettant en évidence le lien entre les wedges 2x2, 2x3 et le premier triangle de Pythagore est d'une harmonie époustouflante !
Notes :
- Le petit montage qui n'est pas un triangle montre que arctan(1/3) + arctan(1/2) = 45°. Ainsi arctan(1/3) + 2 x arctan(1/2) + arctan(1/3) = 90°
- L'absence de wedge 2x6 au profit des 3x12 - qui ont le même angle, arctan(1/6) - contraignent l'esthétique du dernier montage.
Méditez bien sur tout ça, à bientôt !
.gif)
PS : Au passage, si le sujet vous intéresse et que vous voulez mieux le comprendre pour mieux le mettre en oeuvre, j'ai publié un livre à ce propos en mars :
https://messagedelanuitdestemps.org/liv ... re-coussy/
Ne fuyez pas
 , il se veut très pédagogique et très accessible.
, il se veut très pédagogique et très accessible. .gif)
Les commandes peuvent aussi passer directement par moi : [email protected]





















.gif)





 )
)