
D'abord, un planimètre est un outil mécanique qui permet de calculer l'aire d'une surface fermée par balayage de son périmètre. A quoi ça sert ? Et bien à calculer l'aire sous la courbe de certaines fonctions mathématiques, à calculer les moments d'inerties mais aussi à résoudre des problèmes de géométrie. Les ingénieurs d'autrefois (18ème siècle) utilisaient ces instruments pour résoudre des problèmes. Par exemple, à l’évènement des machines à vapeur, il était possible d'obtenir la courbe de la pression et du volume ou des efforts mais ce qui est réellement intéressant et la puissance de cette machine. Grâce à un planimètre, on peut la calculer en parcourant à l'aide du curseur la courbe et obtenir la puissance, bien utile pour les caractériser et les améliorer.

Ok mais un planimètre polaire c'est quoi ? Et bien comme son nom l'indique, ce planimètre fonctionne en coordonnée polaire, c'est à dire que le déplacement du bras d'intégration se fait au moyen d'une rotation et non d'une translation.
Ok mais un planimètre de pritz c'est quoi ? Et bien c'est un planimètre très spécial basé sur un concept qui approxime les aires plutôt qu'il ne les calcule réellement. Comment ? Et bien le curseur du planimètre qui est monté sur un chariot mobile avec une roue suit le périmètre de la surface. La roue peut rouler sans problèmes mais elle est suffisamment massive pour qu'on ne puisse pas la faire déraper (le long de son axe de rotation). En parcourant la courbe avec le curseur, le bras suit alors la courbe, et il suit une courbe particulière, la tractrice.
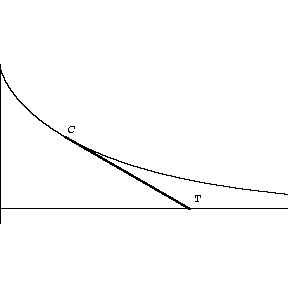

Cette tractrice est un peu comme la dérivé (attention ce n'est pas exactement la dérivé). Par exemple en parcourant une ellipse sur le dessin suivant, on voit bien que la tige reste toujours tangent à la courbe au début, puis rebrousse et revient tangent :
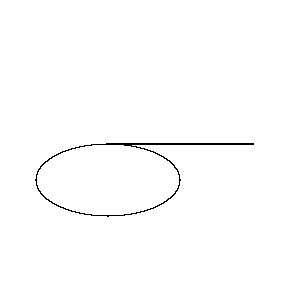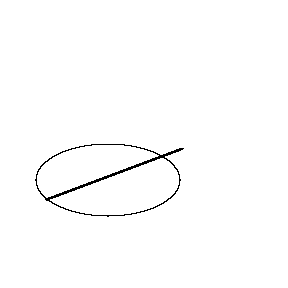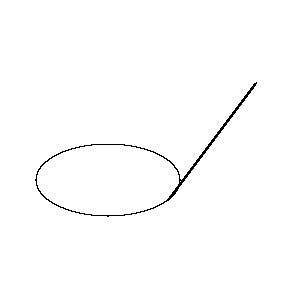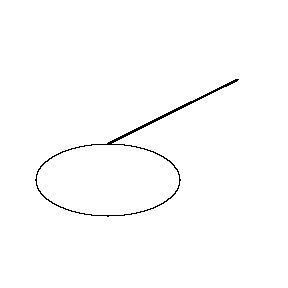
C'est du au fait que la roule puisse rouler mais pas glisser. Sur le planimètre polaire orignal, la roue est remplacée par une fine lame de métal qui vient couper le papier. Elle peut se déplacer le long de la lame mais pas dans l'autre sens (comme une roue très fine). Comme ceci :

Ma création est une adaptation de ce planimètre avec l'ajout d'un bras polaire de renvoi et du cadran. Maintenant pourquoi le fait de parcourir une courbe avec une tractrice fait que sa calcule l'aire ? Et bien c'est des maths et ça vient du théorème de Green qui dit que l'intégral curviligne (aire sous la courbe) d'une surface correspond à son intégral double (son aire) et dans ce cas la c'est une approximation, la différence de position angulaire initiale et final est à peu prés égal à l'aire balayé.

En utilisation, on parcourt du coin inférieur gauche la surface puis on revient au point de départ en fermant la surface, la mesure indiquée par la cardan est l'aire de la surface. Et ce qui est fort, c'est que ça ne dépend ni de l'orientation de la surface ni de sa forme. Je le montre dans le vidéo.

Au niveau du système de bras, l'orientation final du bras est transférée au cadran via un double bras qui entraîne une 40t, connecté à une 8t, connecté au curseur. Il n'y a rien de plus simple et cela assure une démultiplication pour voir les choses puisque l'oscillation du bras n'est que de 0-45°. Au delà, la précision devient médiocre.

La précision, parlons en, que vaut elle ? Bah c'est pas mal, mon planimètre est précis à 5cm² je dirais. En fait, l'erreur vient déjà du fait que la tractrice n'est pas la dérivé exacte, de plus, le système pour transférer l'orientation du bras au cadran est un système de bielle, il est linéaire jusqu’à un certain point, au delà on observe une trop grande erreur car on est très proche du point de rebroussement du système. Le mieux serait un système de parallélogramme mais incompatible avec les déplacement du chariot.
La difficulté reste de tarer le système pour qu'il donne des mesures fiables. Déjà plus le bras polaire est long, meilleur est la précision (peu d'erreur de mesure) mais moins les déplacements sont importants donc plus le jeu parasite la mesure. Il faut donc trouver un optimum pour qu'on voie suffisamment de chose, mais sans trop perdre de précision, en gardant un minimum pour vaincre le jeu. C'est pourquoi la longueur ainsi que les positions des bras de renvois, du bras polaire, des points de pivot sont des données importantes pour bien configurer le planimètre. C'est la dessus que j'ai passé le plus de temps.
Au final qu'est ce que c'est ? Et bien c'est un instrument super intéressant, super simple et qui cache bien son jeu !
Pour récompenser ceux qui ont tout lu :
ps : ce planimètre n'est que le premier d'une longue série.
.gif)











.gif)
























 ): Ca marche aussi si tu fait un "huit" pendant la mesure ?
): Ca marche aussi si tu fait un "huit" pendant la mesure ?

